Du befindest Dich auf der Seite Gemeinde/Investition!

Die Investition
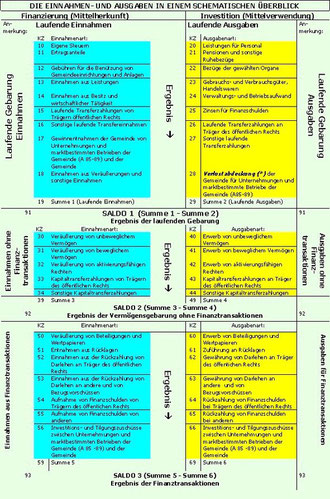
Dieses Bild zeigt die Einnahmenkategorien (=Finanzierung = Mittelherkunft) und die Ausgabenkategorien (=Investition = Mittelverwendung) mit den Kennzahlen der Querschnittsrechnung.
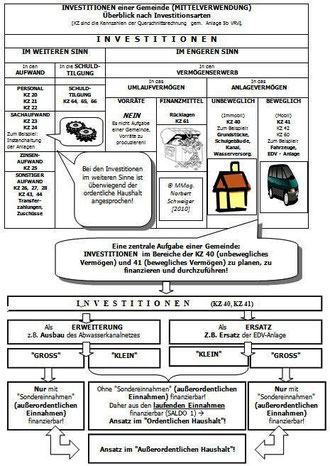
Dieses Bild zeigt eine Überblickstruktur über die möglichen Investitionsarten einer Gemeinde samt den dazugehörigen Kennzahlen der Querschnittsrechnung.
Im unteren Teil des Bildes wird versucht, den Unterschied zwischen den Begriffen "ordentlicher Haushalt" und "ausserordentlicher Haushalt" kurz und bündig herauszuarbeiten.
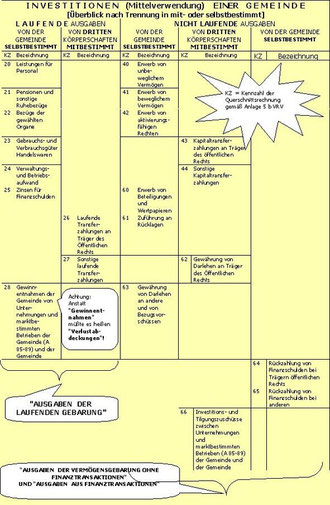
Diese Struktur unterteilt die möglichen Investitionsarten nach den Kriterien
(a) von der Gemeinde selbst bestimmt
(b) von Dritten mitbestimmt
Anmerkung: Bei der Kennzahl 28 müsste es im Falle von Ausgaben meiner Meinung nach sprachlich richtig "Verlustabdeckung" statt "Gewinnentnahmen" heißen.
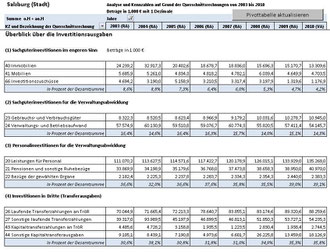
Auf diesem Bild siehst Du den ersten Teil der Investitionsentwicklung der Mozartstadt Salzburg von 2003 bis 2010.
Diese Einteilung bzw. diese Begriffe sieht die VRV so nicht vor! Diese ist meine eigene "Erfindung"!
Folgende Einteilung wird vorgenommen:
(a) Sachgüterinvestitionen im engeren Sinn
(b) Sachgüterinvestitionen für die Verwaltungsabwicklung
(c) Personalinvestitionen für die Verwaltungsabwicklung
(d) Investitionsausgaben in Dritte (Transferausgaben)
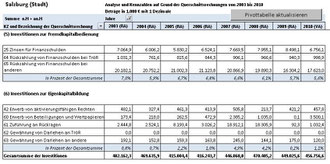
Die Fortsetzung der Investitionseinteilung:
(e) Investitionen zur Fremdkapitalbedienung
(f) Investitionen zur Eigenkapitalbildung
Ich sehe in dieser Einteilung große Vorteile für die Analyse und für die Schlüsse, die daraus gezogen werden können.
Wie siehst Du das? Schreibe mir bitte Deine Meinung über das Kontaktformular!
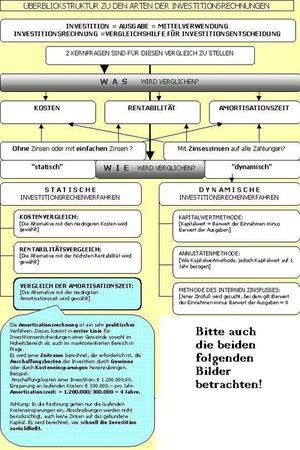
Diese Bild zeigt einen ersten Überblick über die Arten der Investitionsrechnungen.
(1) Was wird verglichen?
a) Kosten?
b) Rentabilität? (=Verzinsung des eingesetzten Kapitals)
c) Amortisationszeit? (in welchem Zeitraum ist das eingesetzte Kapital zurückgeflossen?)
(2) Wie wird verglichen?
a) Statisch (ohne Zinsen oder mit einfachen Zinsen?)
b) Dynamisch (mit Zinsezinsen auf alle Zahlungen?)
Die Ermittlung der Amortisationszeit ist das einfachste Verfahren und neben sehr effizient!
(Siehe das Beispiel in der blauen Legende!)

In diesem Bild werden die statischen Verfahren näher beleuchtet!

Hier gibt es die Kernaussagen zu den dynamischen Verfahren. Die Rechenverfahren sind wunderbar (in der Theorie) anzuwenden!
Das Schwierige daran ist, die dafür zugrunde liegenden Daten zu ermitteln!

 Die neue Staatsverrechnung in Österreich
Die neue Staatsverrechnung in Österreich